Question

Hello! High school student in Calculus here. I need help solving the problem attached in the image. If someone could help break down the steps and explain how to solve the problem using BOTH the product rule AND quotient rule methods (because my teacher advised us to learn how to solve both ways), I would greatly appreciate it!

Answer 1

To find the derivative of the function given we can use the product rule and the quotient rule.

Product rule:

The product rule states that:

`(d)/(dx)(fg)=g(df)/(dx)+f(dg)/(dx)`

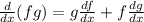
Then, for the function given we have:

`\begin{gathered} (d)/(ds)\lbrack(s^3+4)(4s^2+6)\rbrack=(4s^2+6)(d)/(ds)(s^3+4)+(s^3+4)(d)/(ds)(4s^2+6) \\ =(4s^2+6)(3s^2)+(s^3+4)(8s) \\ =12s^4+18s^2+8s^4+32s \\ =20s^4+18s^2+32s \end{gathered}`

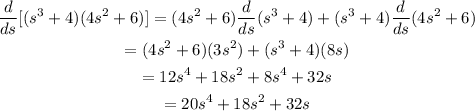
therefore the derivative is:

`(dg)/(ds)=20s^4+18s^2+32s`

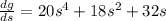
Quotient rule:

To use the quotient rule we need to write the function in the following way:

`g(s)=(s^3+4)/((4s^2+6)^(-1))`

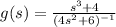
Now, the quotient rulre states that:

`(d)/(dx)((f)/(g))=(g(df)/(dx)-f(dg)/(dx))/(g^2)`

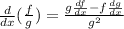
Then, in our case we have:

`\begin{gathered} (d)/(ds)((s^3+4)/((4s^2+6)^(-1)))=((4s^2+6)^(-1)(d)/(ds)(s^3+4)-(s^3+4)(d)/(dx)(4s^2+6)^(-1))/(\lbrack(4s^2+6)^(-1)\rbrack^2) \\ =\frac{(4s^2+6)^(-1)(3s^2)-(s^3+4)\lbrack-(4s^2+6)^(-2)\rbrack^{}(8s)}{\lbrack(4s^2+6)^(-1)\rbrack^2} \\ =((3s^2)/(4s^2+6)+(8s(s^3+4))/((4s^2+6)^2))/(\lbrack(4s^2+6)^(-1)\rbrack^2) \\ =((1)/(4s^2+6)(3s^2+(8s^4+32s)/(4s^2+6)))/(\lbrack(4s^2+6)^(-1)\rbrack^2) \\ =((1)/(4s^2+6)((3s^2(4s^2+6)+8s^4+32s)/(4s^2+6)))/(\lbrack(4s^2+6)^(-1)\rbrack^2) \\ =((1)/(4s^2+6)((12s^4+18s^2+8s^4+32s)/(4s^2+6)))/(\lbrack(4s^2+6)^(-1)\rbrack^2) \\ =((1)/(4s^2+6)((20s^4+18s^2+32s)/(4s^2+6)))/(\lbrack(4s^2+6)^(-1)\rbrack^2) \\ =((20s^4+18s^2+32s)/((4s^2+6)^2))/((1)/((4s^2+6)^2)) \\ =((4s^2+6)^2(20s^4+18s^2+32s))/((4s^2+6)^2) \\ =20s^4+18s^2+32s \end{gathered}`

therefore the derivative is:

`(dg)/(ds)=20s^4+18s^2+32s`

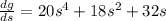
(Notice how we get the same result as before)