The solutions for the compound inequality are (-8,4) or -8 < x < 4
To solve this, lets divide the inequality in two cases:
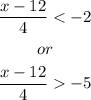
Then let's solve each separeately:
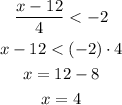
Now for the second part:
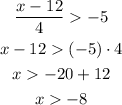
The the solutions are all x that are bigger than -8 and smaller than 4. We can write this like x = (-8,4) or -8< x < 4