Question

2.A rental car company has a special deal on one of the$21.50available rentals. Let C be the cost, in dollars, of the+ $0.45 per mirental car as a function of the distance d, in miles, it isdriven in one day.A. What would the value C(75) represent in this context?B. Is function C increasing or decreasing? What are theunits of the slope in this situation?C. Identify any maximum or minimum values of thefunction. What do they represent in this situation?State any assumptions that youmake.D. Would the graph of C have any intercepts? What would they represent in thissituation?GraphE. Write a rule for C(d), and sketch a graph of the function.

Answer 1

Daily rental = $21.50

cost per miles = $0.45

Let

C = Total cost

d= distance in miles

Therefore, the function can be represented below

`\C=21.50+0.45d`

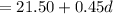
A. The question asked for the total cost for a journey of 75 miles

`\begin{gathered} C=21.50+0.45(75) \\ C=21.50+33.75 \\ C=\text{ \$}55.25 \end{gathered}`

B. The question asked whether function C is increasing or decreasing. The function C is definitely increasing as distance in miles increases. The slope is 0.45.

D. Using the formular the intercept can be found below

`\begin{gathered} y=mx+c \\ \text{where} \\ m=\text{slope} \\ c=y-\text{intercept} \\ \C=21.50+0.45d \\ \text{Intercept = 21.50 } \\ \text{The intercept would represent when the person covers no miles} \end{gathered}`

E. C(d) = 21.50 + 0.45d

Let us sketch a graph where d = 5, 10, 15 , 20 and 25 miles

C(d) = 21.50 + 0.45(5) = 23.75

C(d) = 21.50 + 0.45(10) = 26

C(d) = 21.50 + 0.45(15) = 28.25

C(d) = 21.50 + 0.45(20) = 30.5

C(d) = 21.50 + 0.45(25) = 32.75