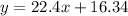When we write a line equation, it can be written in point-slope form. This form is
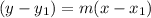
Where m represents the slope of the line, and (x1, y1) are the coordinates of a given point of the line.
Since we already have the slope and point, we can just substitute them on this form.
The line equation written in point-slope form is

The slope-intercept form is

Where m represents the slope and b the y-intercept.
Since we already have the equation in point-slope form, we can just rewrite the equation
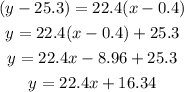
And this is our equation in slope-intercept form