Question

One linear function, t(x), can be modeled by the values in the table below. A second linear function can be modeled by the equation 3x − 2y − 6 = 0. When comparing the x-intercepts of these lines, which function has the largest x-intercept and what is this value?

Answer 1

Step-by-step explanation

The x-intercept of a function is the point where the graph of the function meets the x-axis. At this point the y-value of the function is equal to 0. Then if r is the x-intercept of a linear function its corresponding point in the graph is (r,0).

By looking at the table you'll notice that the point with an y-value of 0 is (4,0) which means that the x-intercept of t(x) is 4.

For the x-intercept of the other function we can just take y=0 on its equation and then solve it for x. With y=0 we obtain:

`\begin{gathered} 3x-2y-6=0\rightarrow3x-2\cdot0-6=0 \\ 3x-6=0 \end{gathered}`

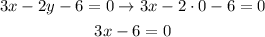
We can add 6 to both sides:

`\begin{gathered} 3x-6+6=0+6 \\ 3x=6 \end{gathered}`

Then we divide both sides by 3:

`\begin{gathered} (3x)/(3)=(6)/(3) \\ x=2 \end{gathered}`

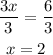
So the x-intercept of 3x-2y-6=0 is 2.

Answer

Then the answer is the third option.