Question

Hello I am trying to solve a matrice problem but I can't seem to find the answer. it's multiplying a 3x2 x 2x2 matrice. But the answer keeps coming incorrect. So it would look like this:First matrice 3x2 matrice 1) 4, 02) -1 ,23) -3, -1xSecond matrice2X2 matrice1) 0, 12) -3, 1I can't seem to understand what I am doing wrong? I am sorry for the format but I wasn't sure how to explain it better.

Answer 1

The given multiplication of matrices is:

`\begin{bmatrix}{4} & {0} & {} \\ {-1} & {2} & {} \\ {-3} & {-1} & {}\end{bmatrix}\cdot\begin{bmatrix}{0} & {1} \\ {-3} & {1}\end{bmatrix}`

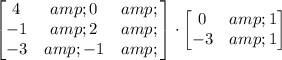
To multiply matrices, we need to multiply the first row in the first matrix, by the first column in the second matrix, term by term and then add them. It would be the first number in the result matrix:

`\begin{bmatrix}{4\cdot0+0\cdot-3} & {\square} & {} \\ {\square} & {\square} & {} \\ {\square} & {\square} & {}\end{bmatrix}=\begin{bmatrix}{0+0} & {\square} & {} \\ {\square} & {\square} & {} \\ {\square} & {\square} & {}\end{bmatrix}=\begin{bmatrix}{0} & {\square} & {} \\ {\square} & {\square} & {} \\ {\square} & {\square} & {}\end{bmatrix}`

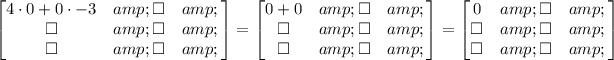
Now, let's do the same procedure for each row and column as follows:

`\begin{bmatrix}{4} & {0} & {} \\ {-1} & {2} & {} \\ {-3} & {-1} & {}\end{bmatrix}\cdot\begin{bmatrix}{0} & {1} \\ {-3} & {1}\end{bmatrix}=\begin{bmatrix}{4\cdot0+0\cdot-3} & {4\cdot1+0\cdot1} & {} \\ {-1\cdot0+2\cdot-3} & {-1\cdot1+2\cdot1} & {} \\ {-3\cdot0+(-1)\cdot(-3)} & {-3\cdot1+(-1)\cdot1} & {}\end{bmatrix}`

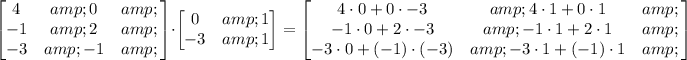
And now, let's solve each expression:

`\begin{gathered} \begin{bmatrix}{4\cdot0+0\cdot-3} & {4\cdot1+0\cdot1} & {} \\ {-1\cdot0+2\cdot-3} & {-1\cdot1+2\cdot1} & {} \\ {-3\cdot0+(-1)\cdot(-3)} & {-3\cdot1+(-1)\cdot1} & {}\end{bmatrix}=\begin{bmatrix}{0+0} & {4+0} & {} \\ {0+(-6)} & {-1+2} & {} \\ {0+3} & {-3+(-1)} & {}\end{bmatrix} \\ \begin{bmatrix}{0+0} & {4+0} & {} \\ {0+(-6)} & {-1+2} & {} \\ {0+3} & {-3+(-1)} & {}\end{bmatrix}=\begin{bmatrix}{0} & {4} & {} \\ {-6} & {1} & {} \\ {3} & {-4} & {}\end{bmatrix} \end{gathered}`

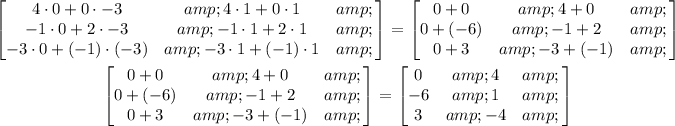
The answer is option C.