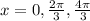Question

Which of the following are the solutions of tan²x + secx = 1 on the interval [0, 2л)?

Answer 1

`x=0,(2\pi)/(3),(4\pi)/(3)`

Explanation:

Given the trigonometric equation:

`tan^2x+secx=1`

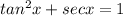
We are required to find the solutions on the interval [0, 2π).

First, recall the trigonometric identity below:

`\tan^2x=\sec^2x-1`

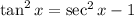
Substitute the identity above for tan²x in the given equation.

`\begin{gathered} tan^(2)x+secx=1 \\ \sec^2x-1+secx=1 \\ \sec^2x-1+\sec x-1=0 \\ \implies\sec^2x+\sec x-2=0 \end{gathered}`

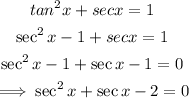
Factorize the resulting quadratic equation:

`\begin{gathered} \sec^2x+2\sec x-\sec x-2=0 \\ \sec x(\sec x+2)-1(\sec x+2)=0 \\ (\sec x-1)(\sec x+2)=0 \end{gathered}`

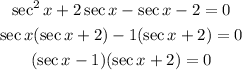
Thus:

`\begin{gathered} \sec x-1=0,\sec x+2=0 \\ \sec x=1,\sec x=-2 \end{gathered}`

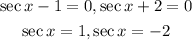
Finally, we solve for x in the interval [0, 2π):

`\begin{gathered} x=\sec^(-1)1=0\in[0,2\pi) \\ x=\sec^(-1)(-2)=(2\pi)/(3),(4\pi)/(3) \end{gathered}`

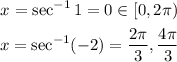
The solutions to the equation on the given interval are:

`x=0,(2\pi)/(3),(4\pi)/(3)`