A 45 - 45 - 90 triangle appears to be an isosceles triangle. This means that the two sides of the triangle are equal.
Putting more details in the figure, we get:
Since the figure is a right triangle, we can use the Pythagorean Theorem to find x.
We get,
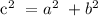
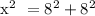
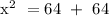
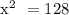
![\text{ x}^{}\text{ }=√(128)\text{ }=\text{ }\sqrt[]{2\text{ x 64}}](https://img.qammunity.org/2023/formulas/mathematics/college/9uwtd7vv20luab55pf445agth4julaazdo.png)
![\text{ x}^{}\text{ }=8\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/saw04lry23ylnnf96jayu98nexep1d3sx8.png)
Therefore, x = 8√2