Finding the width of a rectangle
We know its area and its length
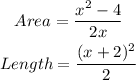
We know
Width · length = area
Let's call w: width, L: length and a: area
Then
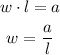
Replacing the given information
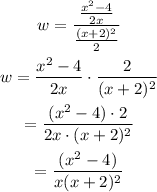
We know that
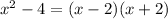
Replacing it in the equation of w
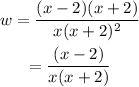
Answer width = (x - 2) / [ x ( x + 2 ) ]