Question

16. The lengths of two line segments are shown. 1in. in. 22 in. 1 1 The length of a third line segment to the nearest 2 inch is 4 z Which statement is true about these three line segments? G. H. These line segments can form a triangle, because each side of the triangle can be a different length These line segments can form a triangle, because the longest side of the triangle can be exactly 4 inches long. These line segments cannot form a triangle, because at least two sides of the triangle must be the same length. These line segments cannot form a triangle, because the longest side of the triangle must be shorter than 4 inches. .

Answer 1

the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side, therefore:

`\begin{gathered} z\le x+y \\ let \\ x=1(1)/(2)=(3)/(2)in \\ y=2(1)/(2)=(5)/(2)in \\ z=4(1)/(2)=(9)/(2)in_{} \end{gathered}`

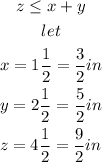
so:

`\begin{gathered} (9)/(2)\le(3)/(2)+(5)/(2) \\ (9)/(2)\le(8)/(2) \\ 4.5\le4 \end{gathered}`

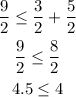
Answer:

These line segments can form a triangle, because the longest side of the triangle can be exactly 4 inches long