Question

Over the last three evenings, Karen received a total of 158 phone calls at the call center. The first evening, she received 8 more calls than the second evening.The third evening, she received 4 times as many calls as the second evening. How many phone calls did she receive each evening?Х5?Number of phone calls the first evening: 0Number of phone calls the second evening: INumber of phone calls the third evening:

Answer 1

Variables

• x: Number of phone calls the first evening

,

• y: Number of phone calls the second evening

,

• z: Number of phone calls the third evening

Given that Karen received a total of 158 phone calls, then:

`x+y+z=158\text{ (eq. 1)}`

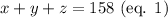
Given that in the first evening, she received 8 more calls than the second evening, then:

`x=8+y\text{ (eq. 2)}`

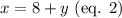
Given that in the third evening, she received 4 times as many calls as the second evening, then:

`z=4y\text{ (eq. 3)}`

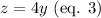
Substituting equations 2 and 3 into equation 1 and solving for y:

`\begin{gathered} (8+y)+y+4y=158 \\ 8+(y+y+4y)=158 \\ 8+6y=158 \\ 8+6y-8=158-8 \\ 6y=150 \\ (6y)/(6)=(150)/(6) \\ y=25 \end{gathered}`

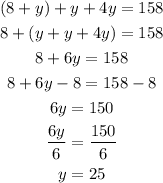
Substituting y = 25 into equations 2 and 3:

`\begin{gathered} x=8+25=33 \\ z=4\cdot25=100 \end{gathered}`

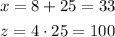
The final answer is:

• Number of phone calls the first evening:, 33

,

• Number of phone calls the second evening: ,25

,

• Number of phone calls the third evening: ,100