Question

Count the possible combinations of 4 numbers chosen from the list (12, 13, 14, 15, 16).answersA) 24B)5C)1D)120

Answer 1

For us to be able to determine the possible combinations of 4 number from the list of 5 numbers (12, 13, 14, 15, 16), we will be using the following formula:

`\text{ C(n,k) = }\frac{n!}{k!(n\text{ - k)!}}`

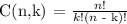
Where,

n = total numbers of sample in the list = 5

k = selected numbers in the list = 4

We get,

`\text{ C(n,k) = }\frac{n!}{k!(n\text{ - k)!}}`
`\text{ C(5,4) = }\frac{5!}{4!(5\text{ - 4)!}}`
`\text{= }\frac{5!}{4!\cdot1\text{!}}`
`\text{= }\frac{(5\text{ x 4 x 3 x 2 x 1)}}{\text{ (4 x 3 x 2 x 1)(1)}}`
`\text{ = }\frac{120}{24\text{ x 1}}\text{ = }(120)/(24)`
`\text{ C(5,4) = 5}`

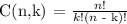
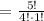
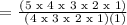
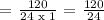
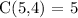
Therefore, the answer is letter B.