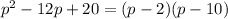To factor a expression of the form:
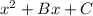
we need to find two integers a and b that fulfills the following conditions:
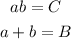
In that way we write the original expression as:
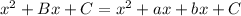
and then we facto by grouping.
Let's make the example to understand this better.

In this case B=-12 and C=20. We need to find two numbers that fulfills:
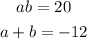
We see that the numbers a=-2 and b=-10, fulfill this conditions. Then we write the expression as:
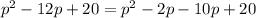
and now we factor the first pair and second pair of terms by common factors:

Therefore: