Given:
The ratio of the volume of the two spheres is 8: 27.
Required:
To find the ratio of their radius.
Step-by-step explanation:
The volume of the sphere is given by the formula:
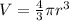
Where r = radius of the circle.
Let the radius of the spheres are

and volume are
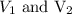
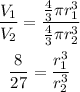
Take the cube root on both sides we get:
![\begin{gathered} (r_1)/(r_2)=\sqrt[3]{(8)/(27)} \\ (r_(1))/(r_(2))=\sqrt[3]{(2*2*2)/(3*3*3)} \\ (r_1)/(r_2)=(2)/(3) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v8miw0nvekc2lj6925tru1noptr11xxpuw.png)
The ratio of their radius is 2 : 3.
Final answer:
Thus option a is the correct answer.