Answer:
P(X > 1) = 0.9970
Step-by-step explanation:
The average number of students, λ = 8
Using the poisson distribution formula:
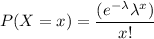
Probability that more than 1 student will have his automobile stolen during the current semester is P(X > 1)
P(X > 1) = 1 - (PX ≤ 1)
P(X≤1) = P(X=0) + P(X=1)
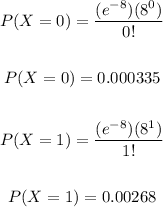
P(X≤1) = 0.000335 + 0.00268
P(X≤1) = 0.003015
P(X > 1) = 1 - (PX ≤ 1)
P(X > 1) = 1 - 0.003015
P(X > 1) = 0.9970