Let
small pizza cost "p"
liter of pop cost "x"
salad cost "y"
From the three statements, we can write 3 equations:
1. Two small pizzas, a liter of pop and a salad cost $28:
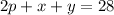
2. one small pizza, a liter of pop, and three salads cost $30:
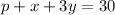
3. three small pizzas, a liter of pop, and two salads cost $44:
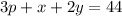
We need to solve these 3 simultaneous equations in order to find the value of "p", "x", and "y".
Multiplying 2nd equation by (-1) and adding it to 1st equation, we get:
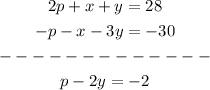
Now, we can multiply the 3rd equation by (-1) and add it to the 2nd equation, we get:
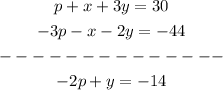
We have 2 new equations. We can multiply this last equation by 2 and add up these 2 new equations. We can solve for p:
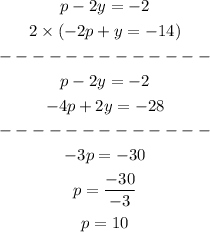
We can take the last equation, put the value of p and find the value of y:
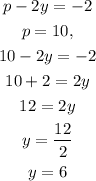
We take first equation (totally first one) and put in the values of p and y and solve for x:
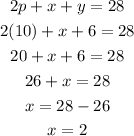
So,
x = 2
y = 6
p = 10
We can say:
one small pizza costs $10
one liter of pop costs $2
one salad costs $6