Question

Find the area of a triangle with legs that are: 9 mm, 6 mm, and 12 mm.A. 11.6 mm²B. 12.3 mm²C. 26.1 mm²D. 37 mm²

Answer 1

We are given that the legs of a triangle to be:

9mm, 6mm, and 12mm.

Solution

We can find the area of a triangle using Heron's formula:

`\begin{gathered} \text{Area = }\sqrt[]{s(s-a)(s-b)(s-c)} \\ \text{where, s = }(a+b+c)/(2) \end{gathered}`

s is called the semi-perimeter, a, b and c are the sides of the triangle.

The semi-perimeter(s) for the given triangle would be:

`\begin{gathered} s\text{ = }(9+6+12)/(2) \\ s\text{ = }(27)/(2) \\ =\text{ 13.5} \end{gathered}`

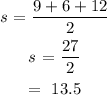
Hence, the area (A) :

`\begin{gathered} A\text{ = }\sqrt[]{13.5(13.5-9)(13.5-6)(13.5-12)} \\ =\text{ }\sqrt[]{13.5*4.5*7.5*1.5} \\ =\text{ 26.1426} \\ =26.1mm^2 \end{gathered}`

Answer: Option C