Question

Two mechanics worked on a car. The first mechanic worked for 10 hours, and the second mechanic worked for 5 hours. Together they charged a total of $1550.What was the rate charged per hour by each mechanic if the sum of the two rates was $ 195 per hour?First mechanic:Second mechanic:Solve by using system of linear equations.

Answer 1

Let x be the rate charged per hour of the first mechanic and let y be the rate charged per hour of the second mechanic.

We know that the first mechanic worked for 10 hours and the second mechanic worked for 5 hours, the total time of work on the car can be express as:

`10x+5y`

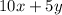
We know that the total amount they charged is $1550, them the expression above is equal to 1550 and we have the equation:

`10x+5y=1550`

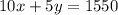
We also know that that the sum of the rates is equal to $195, then we have the equation:

`x+y=195`

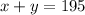
Hence, we have the system of equations:

`\begin{gathered} 10x+5y=1550 \\ x+y=195 \end{gathered}`

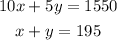
To find the solution of the system let's solve the second equation for y:

`y=195-x`

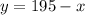
Now we plug this in the first equation and solve the resulting one variable equation for x:

`\begin{gathered} 10x+5(195-x)=1550 \\ 10x+975-5x=1550 \\ 5x=1550-975 \\ 5x=575 \\ x=(575)/(5) \\ x=115 \end{gathered}`

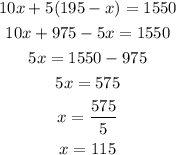
Once we know the value of x we plug in the equation we found for y:

`\begin{gathered} y=195-115 \\ y=80 \end{gathered}`

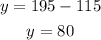
Therefore, the rates charged of each mechanic are:

First mechanic: $115

Second mechanic: $80