Question

Two sides and an angle (SSA) of a triangle are given. Determine whether the given measurements produce one triangle, two triangles, or no triangle at all. Solve each triangle that results.

Answer 1

In this problem, we have a triangle with:

• side a = 8,

,

• side b = 7,

,

• angle A = 30°.

Using the data of the problem, we make the following graph:

From trigonometry, we have the Law of Sines, which states that:

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)\text{.}`

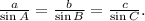
1) Angle B

In particular, we have:

`(a)/(\sin A)=(b)/(\sin B)\text{.}`

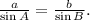
Replacing the values of a, b and A, we have:

`\begin{gathered} (8)/(\sin(30^(\circ)))=(7)/(\sin B), \\ \sin B=(7)/(8)\cdot\sin (30^(\circ)), \\ \sin B=(7)/(16)\text{.} \end{gathered}`

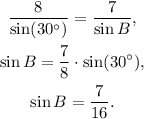
We want to find the values of B in the interval 0 < B < 180° that satisfies the equation above. Solving the equation we get the following values:

`\begin{gathered} B_1\approx26^(\circ), \\ B_2\approx154^(\circ)\text{.} \end{gathered}`

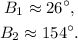
Now, from geometry we know that the inner angles of a triangle must sup up 180°, so the second angle B2 = 154° cannot be a possible answer, because A = 30°, and:

`A+B_2+C=30^(\circ)+154^(\circ)+C>180^(\circ)\text{.}`

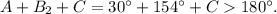
So there is only one possible value for B:

`B\approx26^(\circ)\text{.}`

2) Angle C

We have the angles A = 30° and B = 26°, so angle C is:

`\begin{gathered} A+B+C=180^(\circ), \\ C=180^(\circ)-A-B, \\ C\approx180^(\circ)-30^(\circ)-26^(\circ), \\ C\approx124^(\circ)\text{.} \end{gathered}`

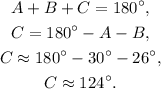
3) Side c

From the Law of Sines, we have:

`(a)/(\sin A)=(c)/(\sin C)\text{.}`

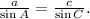
Replacing the values of a, A and C, we have:

`\begin{gathered} (8)/(\sin30^(\circ))\approx(c)/(\sin(26^(\circ))), \\ c\approx8\cdot(\sin(26^(\circ)))/(\sin(30^(\circ))), \\ c\approx7.0 \end{gathered}`

Answers

A. There is only one possible solution to the triangle

• B ≈ 26°

,

• C ≈ 124°

,

• c ≈ 7.0