Question

Solve the following system of equations graphically on the set of axes below(also the solution)

Answer 1

Solution: (-4, 6)

Step-by-step explanation

To solve this system of equations graphically, we have to graph each line. The solution will be the point where the two lines intersect if they do.

To graph the first line, whose equation is given in the slope-intercept form, we can start at the y-intercept, -6, and then find a second point using the slope. Since the slope of this line is -3, from the y-intercept we will "move" 3 units up and, since it is negative, we will move 1 unit to the left. Mark the second point and draw a line through them,

The equation of the second line is given in the standard form. If we solve the equation for y, we will obtain it in slope-intercept form instead,

`\begin{gathered} y=(-x-28)/(-4) \\ \\ y=(1)/(4)x+7 \end{gathered}`

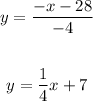
So, following the same steps we did to draw the first line, we have to mark a point at the y-intercept, 7. Then, since the slope is positive, we will "move" 1 unit up and 4 units to the right to find a second point. Mark that point and draw a line through both points,

The lines intersect each other at only one point, so there is only one solution,

Hence, the solution to the system is (-4, 6).