Question

the point G (-7,6), H (-1,4), I (0,7) and J (-6,9) form a quadrilateral. find the desired slopes and lengths then fill in the words that best identifies the type of quadrilateral

Answer 1

To answer this question, we will use the following formulas for the slope and the distance with two given points (x₁,y₁) and (x₂,y₂):

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1), \\ \text{distance}=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}. \end{gathered}`

Applying the above formula for the slope we get:

`\begin{gathered} \text{slopeGH}=(6-4)/(-7-(-1))=-(1)/(3), \\ \text{slopeHI}=(4-7)/(-1-0)=3, \\ \text{slopeIJ}=(7-9)/(0-(-6))=-(1)/(3), \\ \text{slopeJG}=(9-6)/(-6-(-7))=3\text{.} \end{gathered}`

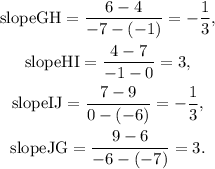
Therefore, GH and IJ are parallel and both are perpendicular to HI and JG. Also, HI and JG are parallel.

Using the formula for the distance we get:

`\begin{gathered} \text{lengthGH}=\sqrt[]{(6-4)^2+(-7-(-1))^2}=\sqrt[]{4+36}=\sqrt[]{40}, \\ \text{lengthHI}=\sqrt[]{(4-7)^2+(-1-0)^2}=\sqrt[]{9+1}=\sqrt[]{10}, \\ \text{lengthIJ}=\sqrt[]{(7-9)^2+(0-(-6))^2}=\sqrt[]{4+36}=\sqrt[]{40}, \\ \text{lengthJG}=\sqrt[]{(9-6)^2+(-6-\mleft(-7\mright))^2}=\sqrt[]{9+1}=\sqrt[]{10}\text{.} \end{gathered}`

Therefore, the parallel sides have the same length.

Answer:

`\begin{gathered} \text{slopeGH}=-(1)/(3), \\ \text{slopeHI}=3, \\ \text{slopeIJ}=-(1)/(3), \\ \text{slopeJG}=3\text{.} \end{gathered}`

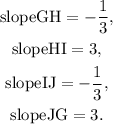
`\begin{gathered} \text{lengthGH}=\sqrt[]{40}, \\ \text{lengthHI}=\sqrt[]{10}, \\ \text{lengthIJ}=\sqrt[]{40}, \\ \text{lengthJG}=\sqrt[]{10}\text{.} \end{gathered}`

The quadrilateral is a rectangle.