Answer:
a)
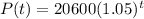
b) 30436
Step-by-step explanation:
An exponential growth function is usually given as;
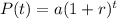
where a = initial amount = 20600
r = rate of increase in decimal = 5% = 5/100 = 0.05
t = time in years
a) So a function that models the population t years after 2020 can be written as;

b) In the year 2028, t = 8, let's go ahead and solve for P(8);
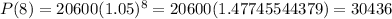
So in the year 2028, the population will be 30436