Question

3.Graph the dilation image of ΔABC,using a scale factor of 1/2 and thecenter of dilation at the origin.

Answer 1

First, identify the coordinates of the points A, B and C:

`\begin{gathered} A=(-2,4) \\ B=(4,2) \\ C=(-2,0) \end{gathered}`

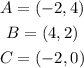
The rule for the transformation of a dilation by a scale factor k is:

`(x,y)\rightarrow(kx,ky)`

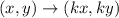
Apply the dilation by a factor of 1/2 to the points A, B and C to find their images A', B', C':

`\begin{gathered} A(-2,4)\rightarrow A^(\prime)((1)/(2)*-2,(1)/(2)*4)=A^(\prime)(-1,2) \\ \\ B(4,2)\rightarrow B^(\prime)((1)/(2)*4,(1)/(2)*2)=B^(\prime)(2,1) \\ \\ C(-2,0)\rightarrow C^(\prime)((1)/(2)*-2,(1)/(2)*0)=C^(\prime)(-1,0) \end{gathered}`

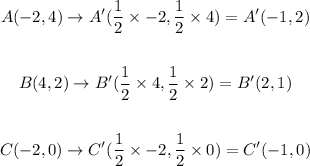
Plot the images A'(-1,2), B'(2,1) and C'(-1,0) to graph the dilation image of the triangle ABC with a scale factor of 1/2: