Question

Use the discriminant test to decide whether the equation represents a parabola, ellipse, or a hyperbola and explain why you know this is true. x^2 - 4xy + 3x + 25y - 6 = 0

Answer 1

Given the equation of a Conic Section:

`x^2-4xy+3x+25y-6=0`

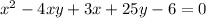
You need to remember that the General Form for a Conic Section is:

`Ax^2+Bxy+Cy^2+Dx+Ey+F=0`

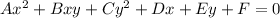
By definition, you can use this formula to find the Discriminant, in order to determine the shape of the Conic Section:

`Discriminant=B^2-4AC`

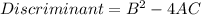
If:

- The Discriminant is negative, then the Conic Section is an Ellipse.

- The Discriminant is greater than zero, then the Conic Section is a Hyperbola.

- The Discriminant is zero, then the Conic Section is a Parabola.

In this case, you can identify that:

`\begin{gathered} A=1 \\ B=-4 \\ C=0 \end{gathered}`

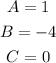
Therefore, by substituting values into the formula and evaluating, you get:

`Discriminant=(-4)^2-4(1)(0)C`
`Discriminant=16`

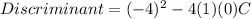
Notice that the discriminant is greater than zero. Therefore the Conic Section is a Hyperbola.

Hence, the answer is: It represents a Hyperbola because the Discriminant is greater than zero.