Consider the equation of the circle below. x ^(2) + {y}^(2) + 8x - 12y + 120 = 144find the center and radius x coordinate of center:y coordinate of center:radius:

Question

consider the equation of the circle below.
`x ^(2) + {y}^(2) + 8x - 12y + 120 = 144`find the center and radius x coordinate of center:y coordinate of center:radius:

Answer 1

Given the following equation:

`x^2+y^2+8x-12y+120=144`

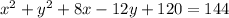
We know that the equation of the circle with radius r and center (h,k) is:

`(x-h)^2+(y-k)^2=r^2`

in this case, we can associate the terms with x and y separately to get the following:

`\begin{gathered} x^2+y^2+8x-12y+120=144 \\ \Rightarrow(x^2+8x)+(y^2-12y)=144-120=24 \\ \Rightarrow(x^2+8x)+(y^2-12y)=24 \end{gathered}`

next, we can complete the square on both summands to get the following:

`(x^2+8x+16)+(y^2-12y+36)=24+16+36`

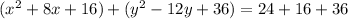
notice that we must add the terms to complete the square on both sides of the equation! IF we factorize the polynomials we get:

`\begin{gathered} (x^2+8x+16)+(y^2-12y+36)=24+16+36_{} \\ \Rightarrow(x+4)^2+(y-6)^2=76 \end{gathered}`

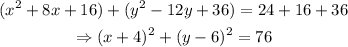
therefore, the x-coordinate of the center is h=-4

the y-coordinate of the ceter is k = 6

the radius is r = sqrt(76)