Question

1. The point (1, - 2) is the vertex of the graph of a quadratic function. Thepoints (0,6) and (2.0) also fall on the graph of the function, Complete thegraph of this quadratic function by first finding two additional points onthe graph.у10-2-8108TO-24-8107Part A: What is the y-intercept of the graphe(0,2).Part B: What are the x-intercepts(5.7370318,0), (0.92963240,0)Part C: Find the interval on which the rate of change is always positive.Part D: What is the sign of the leading coefficient for this quadraticfunction How do you know?

Answer 1

we are asked to determine the equation of a parabola given three points. To do that let's remember the general form of a quadratic equation in vertex form:

`y=a(x-h)^2+k`

Where the point (h, k) is the vertex. We are given that:

`(h,k)=(4,-2)`

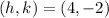
Replacing in the equation we get:

`y=a(x-4)^2-2`

Now, to determine the value of "a" we use the point (2, 0). Replacing we get:

`0=a(2-4)^2-2`

Solving the operations:

`0=4a-2`

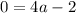
Now we solve form "a" first by adding 2 to both sides:

`\begin{gathered} 2=4a \\ (2)/(4)=a \\ (1)/(2)=a \end{gathered}`

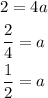
Replacing the value of "a" in the equation:

`y=(1)/(2)(x-4)^2-2`

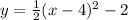
Now the y-intercept is the point where x = 0. replacing that value of "x" in the equation we get:

`y=(1)/(2)(0-4)^2-2`

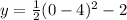
Solving the operations:

`\begin{gathered} y=(1)/(2)(16)-2 \\ y=8-2=6 \end{gathered}`

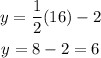
Therefore, the y*