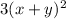So we must factor the following expression:
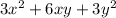
First of all is important to notice that all terms are multiplied by an integer that is a multiple of 3. Then 3 is a common factor and we can re-write the expression like this:
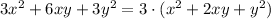
Now let's have a look at the expression inside parenthesis but first let's recall the expression for the square of a binomial. For two real numbers a and b we get:
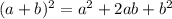
If you replace a and b with x and y we get the following:
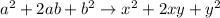
Which means that:
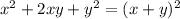
Then the factored form of the original expression and answer to this problem is: