Question

What's the equation of the axis of symmetry of g(x) = x2 + 4x + 3?Question 20 options:A) x = 2B) x = –2C) x = 0D) x = 3

Answer 1

For a parabola equation of the form

`g(x)=a\cdot(x-h)^2+k`

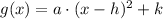
The equation of the symmetry is

`x=h`

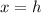
So, rewrite the given equation in the above form as follows:

`\begin{gathered} g(x)=x^2+4x+3 \\ g(x)=x^2+2\cdot x\cdot2+2^2-2^2+3 \\ g(x)=(x+2)^2-4+3 \\ g(x)=(x+2)^2-1 \end{gathered}`

Comparing g(x)=(x+2)^2-1 with g(x)=a(x-h)^2+k one can get, h=-2,k=-1.

So, the axis of symmetry is x=-2.

The correct option is B.