Given that the mass of the rock is, m = 7.51 kg
The height of the bridge is, h = 4.5 m
The potential energy of the rock is
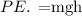
Here, the acceleration due to gravity, g = 9.8 m/s^2
Substituting the values, the potential energy will be
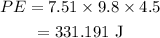
The potential energy will be converted to kinetic energy
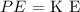
Also, Kinetic energy will be
![\begin{gathered} KE\text{ = }(1)/(2)mv^2 \\ v=\sqrt[]{(2KE)/(m)} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/x0d0ryati3709ghbn469nqn9qyv8fazkrj.png)
Here, v is the speed of the rock.
Substituting the values, the speed of the rock will be
![\begin{gathered} v=\sqrt[]{(2*331.191)/(7.51)} \\ =\sqrt[]{88.2} \\ =9.391\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/p9j4m2xg7zcbtn2s0mr3xd97vycqsbjz0v.png)
The speed of the rock will be 9.391 m/s