Question

b and c please(b) Find the open t-intervals on which the particle is moving to the right. (Enter your answer using interval notation.) Incorrect: Your answer is incorrect.(c) Find the velocity of the particle when the acceleration is 0.21 Incorrect: Your answer is incorrect.

Answer 1

Solving tNow, We are given the following function for the position of a particle:

`x\left(t\right)=t^3-6t^2+9t-7`

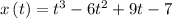
The velocity of the particle is the derivative of the function and is given by:

`x^(\prime)\left(t\right)=3t^2-12t+9`

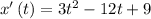
Now, we are asked to determine the interval where the particle is moving to the right. The particle moves to the right when the velocity is positive. To determine the intervals where the velocity is positive we will first determine the points where the velocity is changing directions. The particle changes direction when it is equal to zero, therefore, we set the derivative to zero:

`3t^2-12t+9=0`

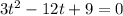
Now, we solve for "t". To do that we will divide both sides by 3:

`t^2-4t+3=0`

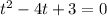
Now, to solve for "t" we will factor the left side. We need to determine two numbers whose product is 3 and their algebraic sum is -4. Those numbers are -3 and -1 since:

`\begin{gathered} -3-1=-4 \\ \lparen-3)\left(-1\right)=3 \end{gathered}`

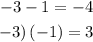
Therefore, the factorization is:

`\left(t-3\right)\left(t-1\right)=0`

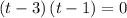
Now, we set each factor to zero:

`\begin{gathered} t-3=0 \\ t=3 \end{gathered}`

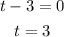
For the second factor:

`\begin{gathered} t-1=0 \\ t=1 \end{gathered}`

Now, we divide the time among these points:

We have three possible intervals for which the velocity can be positive. To determine that we will assign a value of "t" that is smaller than 1 and substitute it in the function for the velocity. Let's take "t = 0". Substituting we get:

`x^(\prime)\left(0\right)=3\left(0\right)^2-12\left(0\right)+9`

Solving we get:

`x^(\prime)\left(0\right)=9>0`

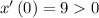
Since the velocity is positive this means that in the interval from 0 to 1 it's moving to the right. This means that in the interval from 1 to 3 it's moving to the left and from 3 to 10 it's moving to the right. Therefore, the intervals are:

`\lparen0,1)\cup\left(3,10\right)`

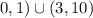
We use parenthesis to indicate that the intervals are open.

Part B. We are asked to determine the velocity when the acceleration is zero. To do that we will set the function for the acceleration to zero and solve for "t".

`x^(\prime)^(\prime)\left(t\right)=6t-12=0`

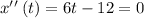
Now, we solve for "t". First, by adding 12 to both sides:

`6t=12`

Now, we divide both sides by 6:

`t=(12)/(6)=2`

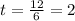
Now, we substitute this value in the formula for the velocity:

`x^(\prime)\left(2\right)=3\left(2\right)^2-12\left(2\right)+9`

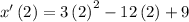
Solving the operations:

`x^(\prime)\left(2\right)=-3`

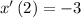
Therefore, the velocity when the acceleration is zero is -3.