Question

I need help with this please show the work Angles l,o,s,p

Answer 1

• l =110°

,

• o= 70°

,

• s = 157°

,

• p = 23°

Explanation:

Angle l

Angles l and 110° form an X-shape. Thus, they are vertical angles.

The measures of vertical angles are equal, therefore:

`l=110\degree`

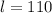
The measure of angle l is 110 degrees.

Angle o

Angles l and o are on the same interior side of a transversal line, thus, l and o are same-side interior angles.

Same-side interior angles are supplementary, i.e. they add up to 180 degrees.

`\begin{gathered} l+o=180\degree \\ 110\degree+o=180\degree \\ o=180\degree-110\degree \\ o=70\degree \end{gathered}`

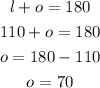
The measure of angle o is 70 degrees.

Angle s

Angles s and 23° are on a straight line.

The sum of angles on a straight line is 180 degrees. Therefore:

The measure of angle s is 157 degrees.

Angle p

Angles p and 23 form a Z-shape. Thus, they are alternate angles.

The measures of alternate angles are equal, therefore:

`p=23\degree`

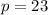
The measure of angle p is 23 degrees.