Answer:
720 pounds per square inch
Step-by-step explanation:
If the stress in the material varies jointly with the internal pressure and the internal diameter and inversely with the thickness of the pipe, we can write the following equation
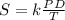
Where S is the stress, P is the internal pressure, D is the diameter, T is thickness, and k is the constant of proportionality.
Then, we know that S = 100 when D = 5, T = 0.75 and P = 25. Replacing the values and solving for k, we get:
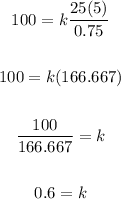
Now, the equation for the stress is
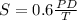
So, we can calculate the strees when P = 80, D = 3 and T = 0.2 as follows
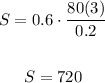
Therefore, the answer is 720 pounds per square inch