Question

Ex4: Bob purchases a new Mercedes S63 AMG for the modest sum of $171,000. Because of its high quality and reputation, the value of this car only decreases by 6% per year.a. Write a general decay model for the value of the car in t years.b. According to the model what is the value of the car in 20 years?C. When does the value of the Mercedes reach half of its original value?

Answer 1

a)

Since the value of the car decreases by 6% each year, then, the car preserves 94% of the value it had the previous year.

Then, after one year, the new price can be found by multiplying the previous price times a factor of 0.94.

After t years, this process occurs t times, then, the final price is the initial price multiplied by (0.94)^t.

Then, a general decay model for the value of the car in t years is:

`y=171,000*0.94^t`

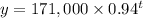
b)

To find the value for the car that this model predicts 20 years in the future, replace t=20:

`\begin{gathered} y_(20)=171,000*0.94^(20) \\ =171,000*0.2901062411\ldots \\ =49,608.16723\ldots \\ \approx49,608.17 \end{gathered}`

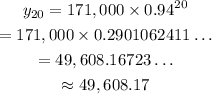
Therefore, the value of the car in 20 years will be $49,608.17 according to the model.

c)

Half of the original value is the same as $85,500.

To find the time that it will take for the car to reach that value, replace y=85,500 and solve for t:

`\begin{gathered} 85,500=171,000*0.94^t \\ \Rightarrow(85,500)/(171,000)=0.94^t \\ \Rightarrow0.5=0.94^t \\ \Rightarrow\log _(0.94)(0.5)=\log _(0.94)(0.94^t) \\ \Rightarrow\log _(0.94)(0.5)=t \\ \therefore t=\log _(0.94)(0.5) \end{gathered}`

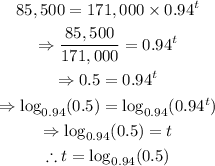
Use a calculator to find a decimal expression for t:

`t=\log _(0.94)(0.5)=11.20230558\ldots\approx11.2`

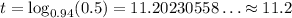
Therefore, the value of the Mercedes will reach half its original value after 11.2 years.