Given function:
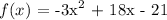
Given the general form of a quadratic equation:
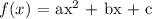
The vertex form of the quadratic equation is:
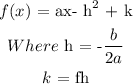
Let us proceed to find the vertex of the quadratic equation:
We have
a = -3, b = 18, c = -21
The x-coordinate of the vertex:
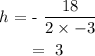
The y-coordinate of the vertex:
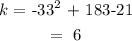
Hence, the vertex of the equation is at (3, 6)
The equation in vertex form is thus:
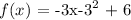
Answer:
The statements that are correct are:
Option A and option E