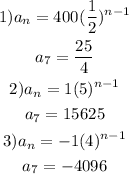Question

Write the rule the nth term; then fing a71) 400, 200, 1002) 1, 5, 25 3) -1, -4, -16

Answer 1

Considering the given Sequences let's find the explicit rule, and then the 7th element:

1) Examining it we can tell this is a Geometric Sequence

`\begin{gathered} (400,\text{ 200, 100)} \\ a_n=a_1q^(n-1)\Rightarrow a_n=400_{}((1)/(2))^(n-1) \\ a_7=400((1)/(2))^(7-1) \\ a_7=(25)/(4) \end{gathered}`

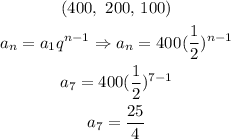
2) We can tell this is another Geometric Sequence whose common ratio is 5

`\begin{gathered} a_n=a_1q^(n-1) \\ a_n=1(5)^(n-1) \\ a_7=5^6 \\ a_7=15625 \end{gathered}`

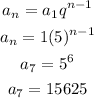
3) Geometric Sequence whose ratio is 4, and the first term is -1:

`\begin{gathered} a_n=a_1q^(n-1) \\ a_n=-1(4)^(n-1) \\ a_7=-1(4)^6 \\ a_7=-4096 \end{gathered}`

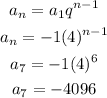
Finally, the answers are:

`\begin{gathered} 1)a_n=400_{}((1)/(2))^(n-1) \\ a_7=(25)/(4) \\ 2)a_n=1(5)^(n-1) \\ a_7=15625 \\ 3)a_n=-1(4)^(n-1) \\ a_7=-4096 \end{gathered}`