.Explanation
Let the speed of the still wind be V
let the speed of the wind be W
From the first statement
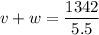
From the second statement
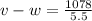
The value of v and w will be obtained by solving using the elimination method
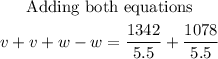
Thus
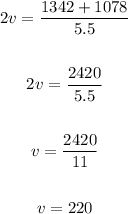
Then to get W
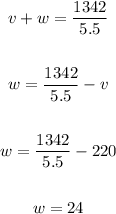
Therefore, the speed of the jet in the still air is 220 miles per hour
The speed of the wind is 24 miles per hour