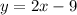Part a
we have the equation
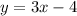
so
The slope is m=3
The y-intercept is the point (0,-4)------> the value of b=-4
To graph the line, we need two points
we have one point (0,-4) y-intercept
Find out another point
For x=1
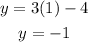
The other point is (1,-1)
so
Plot the points (0,-4) and (1,-10
join them to graph the line
using a graphing tool
see the figure below
Part B
The equation of the line in slope-intercept form is given by
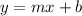
we have (8, 7) and (6, -1)
step 1
Find out the slope
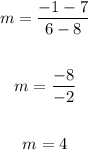
step 2
Substitute given values
we have
m=2
point (8,7)
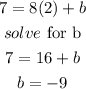
therefore
The equation of the line is