Question

Consider the equations of the following lines: Check carefully that the lines L1 and L2 do not intersect at any point.Verify in detail that the lines L1 and L2 do not intersect at any point."

Answer 1

Given:

`L_1:x-3=(y-2)/(2)=4-z`
`L_2:(x,y,z)=(1,2,1)+s(1,-3,1)`

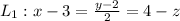
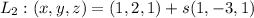
Required:

We need to verify that the lines L1 and L2 do not intersect at any point.

Step-by-step explanation:

Consider the line.

`L_2=(x,y,z)=(1,2,1)+s(1,-3,1)`

`L_2=(x,y,z)=(1,2,1)+(s,-3s,s)`

`L_(2:):(x,y,z)=(1+s,2-3s,1+s)`

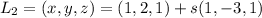
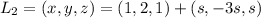
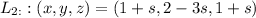
The point (1+s,2-3s,1+s) lies in line 2.

Consider the equation of line 1.

`x-3=(y-2)/(2)`

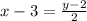
Substitute x =1+s in the equation.

`1+s-3=(y-2)/(2)`

`s-2=(y-2)/(2)`

`2s-4=y-2`

`2s-4+2=y-2+2`
`2s-2=y`

`(y-2)/(2)=4-z`

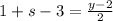
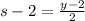
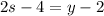
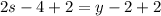
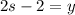
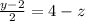
Substitute y =2s-2 in the equation.

`(2s-2-2)/(2)=4-z`

`2s-4=8-2z`

`2s-4-8=-2z`

`2s-12=-2z`
`(2s-12)/(-2)=z`

`6-s=z`

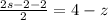
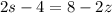
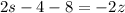
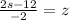
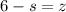
The point (1+s,2s-2,6-s) lies in line 1.

If line 1 and line 2 intersect , then the points should be equal,

Equat the points (1+s,2-3s,1-s) and (1+s,2s-6,6-s).

`(1+s,2-3s,1-s)=(1+s,2s-6,6-s)`

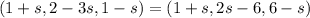
Equate corresponding terms.

`1+s=1+s`
`2-3s=2s-6`
`1-s=6-s`

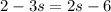
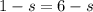
Solve the following equation.

`2-3s=2s-6`

`2+6=2s+3s`

`(8)/(5)=s`

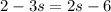
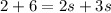
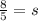
Substitute s =8/5 in the third equation.

`1-(8)/(5)=6-(8)/(5)`

`(5-8)/(5)=(30-8)/(5)`
`-(3)/(5)=(22)/(5)`

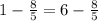
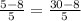
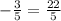
This is not true.

So there is no solution for these equations when we equate the points liying on both line 1 and line 2.

For any value of s, the line does not intersect.

Hence the given lines do not intersect at any point.