Question

Which graph shows a line that is parallel to the line with equation 4x – 8y = 10?

Answer 1

Given: The equation below

`4x-8y=10`

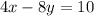
To Determine: From the given graphs, the line that is parallel to the line with the given equation.

Note that parallel lines have the same slope

Calculate the slope of the given equation

`\begin{gathered} 4x-8y=10 \\ 4x-10=8y \\ 8y=4x-10 \\ (8y)/(8)=(4x)/(8)-(10)/(8) \\ y=(1)/(2)x-(5)/(4) \end{gathered}`

The general equation of a line in slope-intercept form is given as

`\begin{gathered} y=mx+c,\text{where} \\ m=\text{slope} \\ c=\text{intercept on the y-axis} \end{gathered}`

Hence, the slope of the given equation is

`\begin{gathered} y=(1)/(2)x-(5)/(4),y=mx+c \\ m(slope)=(1)/(2),c=-(5)/(4) \end{gathered}`

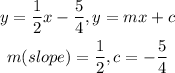
Calulate the slope for each of the given graph by getting 2 points from the graph

OPTION A

`\begin{gathered} point1=(2,0) \\ point2=(0,-2) \\ m=(-2-0)/(0-2)=(-2)/(-2)=1 \end{gathered}`

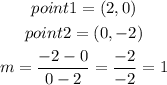
OPTION B

`\begin{gathered} point1=((1)/(2),0) \\ point2=(0,-1) \\ m=(-1-0)/(0-(1)/(2))=(-1)/(-(1)/(2))=(1)/((1)/(2))=2 \end{gathered}`

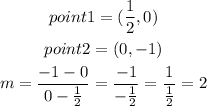
OPTION C

`\begin{gathered} point1=(-1,0) \\ point2=(0,1) \\ m=(1-0)/(0--1)=(1)/(0+1)=(1)/(1)=1 \end{gathered}`

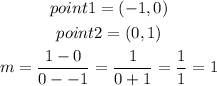
OPTION D

`\begin{gathered} point1=(2,0) \\ point1=(0,-1) \\ m=(-1-0)/(0-2)=(-1)/(-2)=(1)/(2) \end{gathered}`

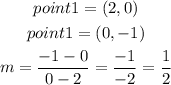
It can be found that only option D has the same slope with the given equation

Hence, the graph that is parallel to the given equation is that of OPTION D