Question

Using the gauss Jordan elimination to solve the systemFind the system solution set

Answer 1

The system solution set is

Step - by - Step Explanation

What to find?

The system solution set of the system of equations.

Given:

x-y+z=-2

3x+y -3z = 16

4x-6y + 7z=-19

To solve using the Gauss - Jordan elimination, we need to first set an argumented matrix.

That is;

`\begin{bmatrix}{1} & {-1} & {1\text2}\text{ } \\ {3} & {1} & {-3\text } \\ {4} & {-6} & {7\text}\end{bmatrix}`

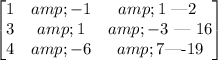
We can now proceed to solve using elementary row operations.

subtract row 1 multiply by 3 from row 2.

That is;

R₂ = R₂ - 3R₁

`\begin{bmatrix}{1} & {-1} & {1\text-2} \\ {0} & {4} & {-6\text 22} \\ {4} & {-6} & {7\text -19}\end{bmatrix}`

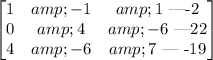
Subtract row 1 multiply by 4 from row 3.

That is;

R₃ = R₃ - 4R₁

`\begin{bmatrix}{1} & {-1} & -2 \\ {0} & {4} & -6 \\ {0} & {-2} & -11\end{bmatrix}`

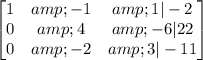
Divide row 2 by 4.

That is

R₂ =R₂/4

`\begin{bmatrix}{1} & {-1} & -2 \\ {0} & {1} & -(3)/(2) \\ {0} & {-2} & -11\end{bmatrix}`

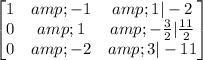
Add row 2 to row 1.

That is;

R₁ =R₁ + R₂

`\begin{bmatrix}{1} & {0} & -(1)/(2) \\ {0} & {1} & -(3)/(2 \\ {0} & {-2} & 3\end{bmatrix}`

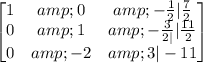
Add row 2 multiply by 2 to row 3.

That is;

R₃ = R₃ + 2R₂