We can find the intervals for which P(x) is increasing or decreasing by evaluating the first derivative P'(x).
We can think of the value of P'(x) as the slope of the tangent line to the curve P(x).
The tangent line has negative slope when P(x) is decreasing and positive slope when P(x) is increasing.
Then, the sign of P'(x), as it is the sign of the slope, tells us if P(x) is increasing or decreasing.
We can find P'(x) as:
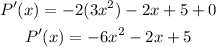
If we calculate the roots of P'(x) we get:
![\begin{gathered} x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4\cdot(-6)\cdot5}}{2\cdot(-6)} \\ x=\frac{2\pm\sqrt[]{4+120}}{-12} \\ x=\frac{-2\pm\sqrt[]{124}}{12} \\ x\approx(-2\pm11.14)/(12) \\ x_1=(-2-11.14)/(12)=(-13.14)/(12)\approx-1.1 \\ x_2=(-2+11.14)/(12)=(9.14)/(12)\approx0.8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/xnz4cl20dx5aylvbi9dmyis8apray5z5k1.png)
As the quadratic coefficient a=-6 is negative, we can conclude that P'(x) is negative for x<-1.1 and x>0.8.
Then, P'(x) is positive for -1.1
Then, we can conclude:
P(x) is increasing in the interval -1.1P(x) is decreasing in the intervals x<-1.1 and x>0.8
Answer: [Option C] increasing in -1.10.8