Question

Find from the first principles the derivatives of the following y=x raise the power negative 2

Answer 1

We have to find the derivative of y = x^(-2) using the first principles. This means that we have to calculate the derivative from the limit of the secant line.

We can then write:

`\begin{gathered} f^(\prime)(x)=\lim_(h\to0)(f(x+h)-f(x))/(h) \\ f^(\prime)(x)=\lim_(h\to0)((x+h)^(-2)-x^(-2))/(h) \end{gathered}`

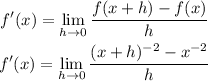
We can rearrange the expression first and then calculate the limit:

`\begin{gathered} (1)/(h)[(1)/((x+h)^2)-(1)/(x^2)] \\ (1)/(h)[(x^2-(x+h)^2)/((x+h)^2x^2)] \\ (1)/(h)((x^2-x^2-2xh-h^2)/((x+h)^2x^2)) \\ (1)/(h)((-2xh-h^2)/((x+h)^2x^2)) \\ (-2x-h)/((x+h)^2x^2) \end{gathered}`

We can now calculate the limit as:

`\lim_(h\to0)(-2x-h)/((x+h)^2x^2)=(-2x-0)/((x+0)^2x^2)=(-2x)/(x^4)=-(2)/(x^3)`

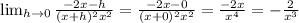
Answer: the first derivative is -2/x³