Question

Hi I need help with this question real quick this I’m having trouble with solving and answering

Answer 1

Step-by-step explanation

We can do the following steps to solve the exercise.

Step 1: We can use the exterior angle theorem to find the value of x. This theorem state that the exterior angle is equal to the sum of the two opposite interior angles.

`d=a+b`

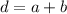
Then, we can write and solve for x the following equation.

`\begin{gathered} (7x+10)\degree=(2x+40)\degree+(3x)\degree \\ (7x)\degree+10\degree=(2x)\degree+40\degree+(3x)\degree \\ (7x)\degree+10\degree=(5x)\degree+40\degree \\ \text{ Subtract 10\degree from both sides} \\ (7x)\degree+10\degree-10\degree=(5x)\degree+40\degree-10\degree \\ (7x)\degree=(5x)\degree+30\degree \\ \text{ Subtract (5x)\degree from both sides} \\ (7x)\degree-(5x)\degree=(5x)\degree+30\degree-(5x)\degree \\ (2x)\degree=30\degree \\ \text{ Divide by 2\degree from both sides } \\ ((2x)\degree)/(2\degree)=(30\degree)/(2\degree) \\ x=15 \end{gathered}`

Step 2: Find the measure of angle ABD. For this, we replace the value of x into the expression that represents the measure of angle ABD.

`\begin{gathered} m\angle ABD=(7x+10)\degree \\ m\angle ABD=(7\cdot15+10)\degree \\ m\angle ABD=(105+10)\degree \\ m\angle ABD=115\degree \end{gathered}`

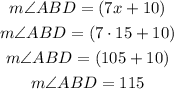
Step 3: Find the measure of angle ABC. Angles ABC and ABD are supplementary angles, that is, they add up 180°. Then, we can write and solve the following equation.

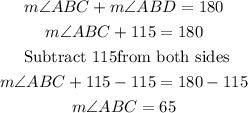
`\begin{gathered} m\angle ABC+m\angle ABD=180\degree \\ m\angle ABC+115\degree=180\degree \\ \text{ Subtract 115\degree from both sides} \\ m\angle ABC+115\degree-115\degree=180\degree-115\degree \\ m\angle ABC=65\degree \end{gathered}`Answer

The measure of angle ABC is 65°.