Question

pe graph of the function /is shown, and consists of two line segments. Let g be the functions given by s6o - Trend a) Find g(-1), g'(-1), "(-1). f fis Stadt رک 03 9 -2 -10 2 b) For what values of x in the open interval (-2, 2) is g increasing? Explain your reasoning from - tol on the axis bus. interval it se starts at an increase then. a declace to finchis the graph. -1 down ito coot -2 c) For what values of x in the open interval (-2, 2) is the graph of g concave down? Explain your reasoning. 012 (-2.-3) -37 (2.-3) Graph of 이 d) On the axes provided, sketch the graph of g on the closed interval (-2,2].

Answer 1

a)

We have the following function given by an integral

`g(x)=\int ^x_0f(t)dt`

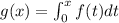
Let's evaluate it at g(-1), we have

`g(-1)=\int ^(-1)_0f(t)dt`

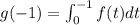
Looking at the graph of f(t) we can see that it's the area of a triangle of base 1 and height 3, therefore

`g(-1)=\int ^(-1)_0f(t)dt=-\int ^0_(-1)f(t)dt=-(3\cdot1)/(2)=-(3)/(2)`

g(-1) is -3/2

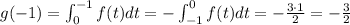
`g(-1)=\int ^(-1)_0f(t)dt=-(3)/(2)`

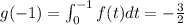
To find the derivative of f(x) we can use the fundamental theorem, therefore

`g^(\prime)(x)=(d)/(dx)\int ^x_0f(t)dt=(d)/(dx)\lbrack F(x)-F(0)\rbrack=f(x)`

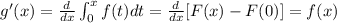
Therefore

`g^(\prime)(x)=f(x)`

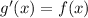
Looking at the graph we can see that, g'(-1) = 0

`g^(\prime)(-1)=f(-1)=0`

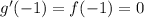
And now for the last derivative, we have

`g^(\prime)^(\prime)(-1)=f^(\prime)(-1)`

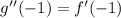
As we can see f(x) is a line of positive slope at the interval (-∞, 0], the derivative of a line if the slope, we can easily see that the slope of f(x) at (-∞, 0] is 3, therefore

`g^(\prime\prime)(-1)=f^(\prime)(-1)=3`

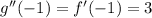
d) Here we will use the fact that f is compounded function (or a modular function), so let's find the expression of f and then do the integral to find g, as we can see, we have a line for (-∞, 0] and another line for [0, ∞), the equations are very easy to find.

For (-∞, 0] we have

`y=3x+3`

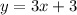
And for [0, ∞)

`y=-3x+3`

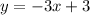
Then we can write the function f

`f(x)=\begin{cases}3x+3,\quad x<0 \\ -3x+3,\quad x\ge0\end{cases}`

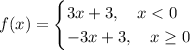
Therefore when we solve the integral for g(x) we will find two different functions, one for x>0 and the other for x<0. then let's do it first for x<0

`\begin{gathered} \int ^x_0f(t)dt,\quad x<0 \\ \\ \int ^x_0(3t+3)dt\Rightarrow(3t^2)/(2)+3t+c\Rightarrow(3x^2)/(2)+3x+c-(3\cdot0^2)/(2)-3\cdot0-c \\ \\ \\ \int ^x_0(3t+3)dt=(3x^2)/(2)+3x \end{gathered}`

Now we will repeat the exact same process but now for x > 0

`\begin{gathered} \int ^x_0f(t)dt,\quad x>0 \\ \\ \int ^x_0(-3t+3)dt\Rightarrow-(3t^2)/(2)+3t+c\Rightarrow-(3x^2)/(2)+3x+c+(3\cdot0^2)/(2)-3\cdot0-c \\ \\ \int ^x_0(-3t+3)dt=-(3x^2)/(2)+3x \end{gathered}`

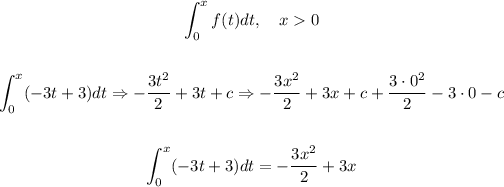
Therefore we have the expression for g now

`\begin{gathered} g(x)=\begin{cases}(3x^2)/(2)+2x,\quad x<0 \\ \\ -(3x^2)/(2)+2x,\quad x\ge0\end{cases} \\ \end{gathered}`

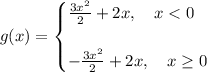
Then to graph g we must graph two quadratics! Let's plot these quadratics from -2 to 2