1. (1/125)^-2/3
Here are the steps in simplifying the given term.
a. Make the exponent positive by getting the reciprocal of the base.
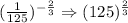
b. Get the cube root of 125.
![\sqrt[3]{125}=5](https://img.qammunity.org/2023/formulas/mathematics/college/ldn2w23r5ntjwsb03ilf4uwjmq5nts9i6g.png)
c. Square the result in step b.
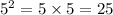
Therefore, (1/125)^-2/3 = 25.
2. 64^-2/3
To simplify this, we follow the same steps shown above.
a. Again, make the exponent positive by getting the reciprocal of the base.
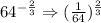
b. Get the cube root of 1/64.
![\sqrt[3]{(1)/(64)}=(1)/(4)](https://img.qammunity.org/2023/formulas/mathematics/college/uqn5ktdjq805csa74o8xhlyfu87ywly8mt.png)
c. Square the result in step b.
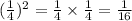
Hence, 64^-2/3 = 1/16.