Answer:
35 and 16.
Step-by-step explanation:
Let the two whole numbers be x and y respectively.
• The product of the two whole numbers is 560: xy=560
,
• Their sum is 51: x+y=51

Substitute x=51-y into xy=560.
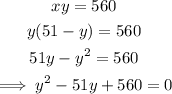
Next, solve the quadratic equation for y:
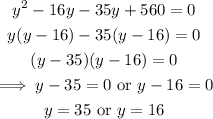
Finally, solve for x:
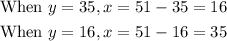
Thus, the two numbers are 35 and 16.