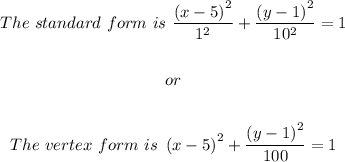Question

Writing an equation of an ellipse given the center an endpoint of an axis and the length of the other axis

Answer 1

Step 1:

The equation of an ellipse is

`((x-h)^2)/(a^2)\text{ + }((y-k)^2)/(b^2)\text{ = 1}`

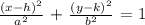
where (h,k) is the center, a and b are the lengths of the semi-major and the semi-minor axes.

Step 2

Thus, h = 5, k=1, a = 1.

The following equation takes into account different properties of an ellipse:

`\begin{gathered} \left(k+9\right)^2=b^2. \\ (1+9)^2=b^2 \\ 10^2\text{ = b}^2 \\ \text{b = 10} \end{gathered}`

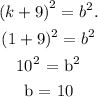
Final answer

`\begin{gathered} The\text{ }standard\text{ }form\text{ }is\text{ }(\left(x - 5\right)^(2))/(1^(2))+(\left(y - 1\right)^(2))/(10^(2))=1 \\ \\ or \\ \\ The\text{ }vertex\text{ }form\text{ }is\text{ }\left(x-5\right)^2+(\left(y - 1\right)^(2))/(100)=1 \end{gathered}`