First, we need to find the volume of the pool.
Use the cylinder volume equation:
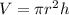
where:
r= radius
h = height
To find the radius r=d/2, then r=9m/2 = 4.5m.
and the height is the depth = 1.7
Replace using the equation:
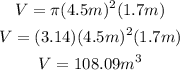
Hence, the pool holds 108.09m³ of water, at a rate of 16m³/hr.
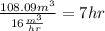
It will take 7 hours to fill the empty pool (The answer is rounded to the nearest hour)