Question

I just need to know the correct one, i’m in a rush

Answer 1

Consider the following implications,

`\begin{gathered} f(-x)=f(x)\Rightarrow\text{ Even Function} \\ f(-x)=-f(x)\Rightarrow\text{ Odd Function} \end{gathered}`

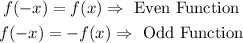
It is required to check that which of the given options satisfy the necessary condition for an even function.

Option A

Consider the function,

`f(x)=\sin (-3\pi x)`

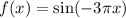
Apply the check,

`\begin{gathered} f(-x)=\sin (-3\pi(-x)) \\ f(-x)=\sin (3\pi x) \\ f(-x)=-\mleft\lbrace-\sin (3\pi x)\mright\rbrace \\ f(-x)=-\sin (-3\pi x) \\ f(-x)=-f(x) \end{gathered}`

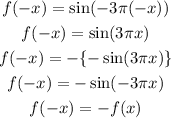
So given function is not an even function.

Option B

Consider the function,

`f(x)=\tan (3\pi x)`

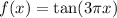
Apply the check,

`\begin{gathered} f(-x)=\tan (3\pi(-x)) \\ f(-x)=\tan \mleft\lbrace-(3\pi x)\mright\rbrace \\ f(-x)=-\tan (3\pi x) \\ f(-x)=-f(x) \end{gathered}`

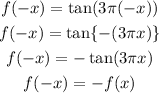
So the given function is akso not an even function.

Option C

Consider the function,

`f(x)=\cos ((5)/(4)\pi x)`

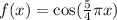
Apply the check,

`\begin{gathered} f(-x)=\cos ((5)/(4)\pi(-x)) \\ f(-x)=\cos \mleft\lbrace-((5)/(4)\pi x)\mright\rbrace \\ f(-x)=\cos ((5)/(4)\pi x) \\ f(-x)=f(x) \end{gathered}`

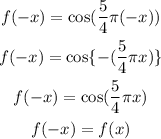
As the condition is satisfied, the given function is an even function.

Thus, option C is the correct choice.