Question

Find the slope of a line that is a) parallel and b) perpendicular to the given line.— 5x — 6у = -7

Answer 1

Parallel lines have the same slopes

The product of the slopes of the perpendicular lines is -1, which means if the slope of one line m, then the slope of the perpendicular line is -1/m (reciprocal it and change its sign)

The form of the linear equation is

`y=mx+b`

m is the slope

Then to find the slope of a line from its equation put the equation in the form above

Since the given equation is

`-5x-6y=-7`

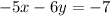
Add 5x to both sides

`\begin{gathered} -5x+5x-6y=-7+5x \\ -6y=-7+5x \\ -6y=5x-7 \end{gathered}`

Now, divide both sides by -6 to make the coefficient of y = 1

`\begin{gathered} (-6y)/(-6)=(5x)/(-6)-(7)/(-6) \\ y=-(5)/(6)x+(7)/(6) \end{gathered}`

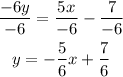
By comparing it by the form of the equation above to find m

`m=-(5)/(6)`

The slope of the given line is -5/6

a) The slope of the parallel line is the same as the slope of the given line

`m_1=m_2=-(5)/(6)`

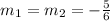
b) to find the slope of the perpendicular line flip the fraction and change its sign

`\begin{gathered} m_1=-(5)/(6) \\ m_2=(6)/(5) \\ m_1* m_2=-(5)/(6)*(6)/(5)=-1 \end{gathered}`

The slope of the perpendicular line is 6/5